平方根算法之四(翻译)

LiHengFeng posted @ 2008年3月22日 23:45 in 算法 , 5925 阅读

本blog所有文章，除声明了作者外，均为原创。欢迎转载，转载请注明作者。

三、手算开平方根

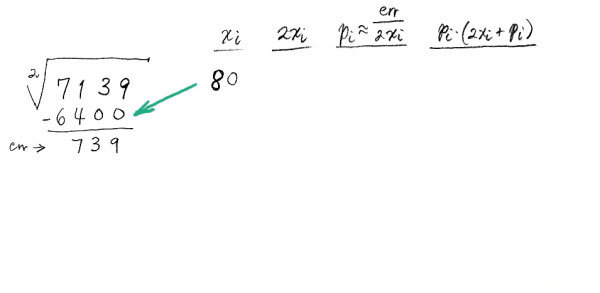
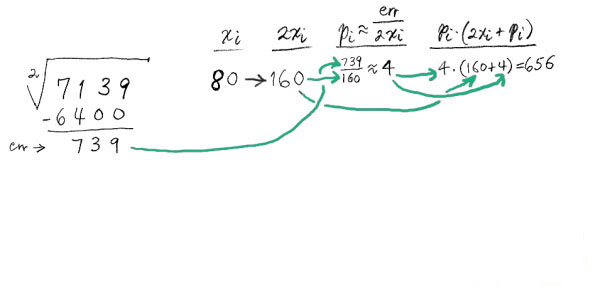
这里，Carl Sagan有一个有意思的评论。在他的书《The Demon Haunted World》里，一个著名的天文学家因为在学校学到了一种手算平方根的方法但却不知道其原理，而责难他就读的公立学校。我们已经在第一节中解释了方法的关键，并称之为第二种近似方法。因此，我们可以在第3步执行一个快速的除法，即执行一个1位近似除法以便简化我们的计算。要执行算法中其它的运算，需要几列的草稿纸空白。让我们用一个手工开平方根的例子作为开始：

为了理解每一步是怎么运算的，请跟随箭头看计算的顺序。如果你在学校学会了手算开平方根的方法，你可能会注意到它和这里的方法有些微小的差别。关于长除法，我总是认为它缺乏效率，并且在学校里教的方法有无法容忍的过度估计。当然有时候，过度估计能得出更加精确的结果。通常，从高估的结果中降低比从低估的结果中进行限制更很容易些。这会使终结步骤，取整步骤更加复杂，不过一般会简化的中间计算。对整数，终结条件是 err<0.5。这可以确保得到正确的平方根截断值。

四、距离估计

在计算机图形学中的一个常见应用是计算出两点之间的距离√(Δx²+Δy²)。然而，因为性能的原因，平方根操作是一个大问题，经常被粗略的近似到一个可接受的程度。因此，我们考虑(1 / √2)*(|x|+|y|)，和 max(|x|,|y|)量度：

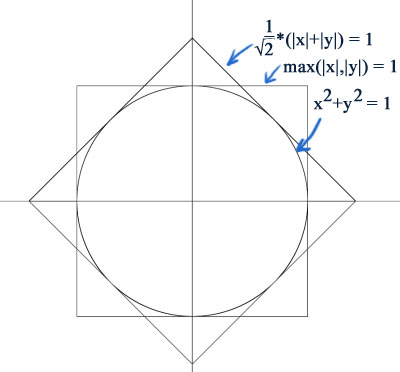
注意到这两个量度围成的八边形，它与通常的距离量度很接近。对应于八边形的量度是：

octagon(x,y) = min ((1 / √2)*(|x|+|y|), max (|x|, |y|))

稍加变换，我们可以得到距离量度在两个八边形量度之间：

octagon(x,y) / (4-2*√2) ≤ √(x²+y²) ≤ octagon(x,y)

上式中，1/(4-2*√2) ≈ 0.8536，它离1不是很远。因此，我们可以利用下面的公式在不进行平方根运算的情况下得到一个粗略的近似值：

distanceapprox (x, y) = (1 + 1/(4-2*√2))/2 * min((1 / √2)*(|x|+|y|), max (|x|, |y|))

这个估计值离真实值偏差最多大约8%。

在三维下类似的公式是：

distanceapprox (x, y, z) = (1 + 1/⁴√3)/2 * min((1 / √3)*(|x|+|y|+|z|), max (|x|, |y|, |z|))

最大误差有大约16%。

然而，有些事情有必要指出。计算距离常常只是为了比较的目的。例如，在经典mandelbrot 集合 (z←z²+c)的计算中。the magnitude of a complex number is typically compared to a boundary radius length of 2. 在这些情况下，可以通过两边同时平方简单的去除平方根运算（因为所有的距离都是非负的）。就是说：

√(Δx²+Δy²) < d 等价于Δx²+Δy² < d²，如果 d ≥ 0。

五、数学理论

5a公式

下面是一些在普通的数学计算中可能用到的平方根相关公式：

      √a*b = √a *√b, if a,b ≥ 0
        ln√a = (½)*ln(a), if a > 0
        √1/a = 1/√a, if a > 0
        √(a²) = |a|
        (√a)² = a, if a ≥ 0
        1/(√a+√b) = (√a-√b)/(a-b), if a,b ≥ 0, a≠b
        1/(√a-√b) = (√a+√b)/(a-b), if a,b ≥ 0, a≠b
        |a + i*b| = √(a²+b²)

其中a，b是实数且the domain restrictions are given (and cannot be ignored).复数平方根可以计算如下：

√a+i*b = ±√((√(a²+b²)+a)/2) ± i*√((√(a²+b²)-a)/2)

注意到每一部分的符号要正确选择，就是说，四种可能中只有两中是正确的。如果b>0，两部分的符号必须是相同的；如果b<0，则两部分的符号必须不同。如果b=0，两部分中只有一个是非零的，符号可以任意。上式不是一个定义，只是计算出一个值的方法，使该值的平方等于给定的数。

5b.简单的数学属性

1.一个完全平方数（一个正整数的平方）等于从1开始的一系列奇数的平方之和。

2.任何正的合数必有一个正因数大于1且小于或者等于该数的平方根。

3.一个正无理数的平方根必为无理数且一个正代数(algebraic)的平方根必为代数。

5c.历史

平方根，作为历史上的一个事件，是很有意思的。它让毕达哥拉斯（Pythagoras）引入了“无理数”的概念。毕达哥拉斯认为所有的数都可以表示为一个分数（即有理数）。但是，他的一个第子，希勃索斯（Hippasus）使用了一种叫做“归谬法(reducto ad absurdum)”（反证法的一种）的方法发现，事实上有些数不能表示为分数：

假定 x/y = √2，x，y都是整数。有x² = 2*y²。但是等式左边有偶数个2的因子，同时等式右边有奇数个2的因子。这是不可能的。因此，最初的假定x/y = √2是错误的。证毕。

这一切发生在学术研究的理念和开放的数学讨论并不普遍提倡的时候。在这个发现以前，毕达哥拉斯和他的追随者们向人们宣称所有的数都可以表达为有理数。当毕达哥拉斯学派发现存在非有理数的时候，他们决定向公众保守秘密并且将发现者希勃索斯杀死。

平方根对毕达哥拉斯当然是很重要的，因为在他的定理中可以用平方根计算出直角三角形的边长。毕达哥拉斯定理最终导致了17世纪法国数学家费马（Pierre de Fermat）考虑相同形式但是指数大于2的变形等式。费马认为xⁿ+yⁿ=zⁿ当n>2时没有非平凡的整数解（著名的费马最后定理），该定理直到1995年才由英国数学家威尔斯（Andrew Wiles）最终给出了证明。

六、致谢

这篇文章中的信息来源于下面这些人的巨大贡献：

Norbert Juffa
Bruce W. Holloway
James Van Buskirk
Mark Borgerding
Vesa Karvonen
Arne Steinarson
Joachim Stadel
Dann Corbit
Mathew Hendry
Lawrence Kirby
Jim Ulery
Mark Crowne
Jeremy M.
Ben S.